Расчет объема цилиндра: формула и приложения

Здание Планетария Тихо Браге, Копенгаген, его крыша является примером цилиндрического сечения

Цили́ндр (др.-греч. κύλινδρος —

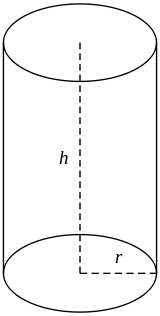
Цилиндром называется геометрическое тело, которое ограничено цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими эту поверхность. Его характеризует отрезок, образованный плоскостями, проходящими через его основания перпендикулярно к ним, или же это значение представляет собой длину такого отрезка.

Связанные определения[править | править код]

• ическая поверхность — поверхность, образуемая однопараметрическим семейством параллельных прямых (называемых образующими) и проходящими через точки некоторой кривой (называемой направляющей).
• Плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями, ограничивающими цилиндр, называются основаниями этого цилиндра.
• Часть цилиндрической поверхности, находящаяся между плоскостями оснований, называется боковой поверхностью цилиндра.
• Высотой цилиндра

Типы цилиндров[править | править код]

• Прямым называется цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), прямая между которыми перпендикулярна плоскостям этих оснований. Данная прямая называется осью цилиндра.
• Косым называется цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), отрезок между которыми не перпендикулярен плоскостям этих оснований.
• Круговым называется цилиндр с окружностью в роли направляющей.
• ом вращения, или прямым круговым цилиндром (часто под цилиндром подразумевают именно его) называется цилиндр, который можно получить вращением (то есть тело вращения) прямоугольника вокруг одной из его сторон, содержащая которую прямая в таком случае будет осью этого цилиндра и его осью симметрии.
• , основания которого являются эллипсами, параболами или гиперболами, называют соответственно эллиптическим, параболическим и гиперболическим; последние два имеют бесконечный объём.
• Призма также является разновидностью цилиндра — с основанием в виде многоугольника.
• Равносторонним называется цилиндр вращения, диаметр основания которого равен его высоте[1].

Свойства[править | править код]

• Если плоскость основания цилиндра параллельна плоскости направляющей, то граница этого основания будет по форме совпадать с направляющей кривой.

Площадь поверхности цилиндра[править | править код]

Площадь боковой поверхности[править | править код]

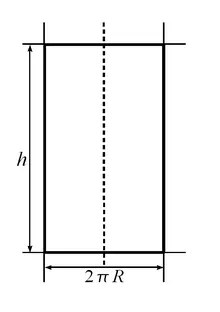
К вычислению площади боковой поверхности цилиндра

Площадь боковой поверхности цилиндра равна длине образующей, умноженной на периметр сечения цилиндра плоскостью, перпендикулярной образующей.

Площадь боковой поверхности прямого цилиндра вычисляется по его развёртке. Развёртка цилиндра представляет собой прямоугольник с высотой и длиной , равной периметру основания. Следовательно, площадь боковой поверхности цилиндра равна площади его развёртки и вычисляется по формуле:

В частности, для прямого кругового цилиндра:

, и , здесь и далее — радиус основания цилиндра.

Для наклонного цилиндра площадь боковой поверхности равна длине образующей, умноженной на периметр сечения, перпендикулярного образующей:

Простой формулы, выражающей площадь боковой поверхности косого цилиндра через параметры основания и высоту, в отличие от объёма не существует. Для наклонного кругового цилиндра можно воспользоваться приближёнными формулами для периметра эллипса, а затем умножить полученное значение на длину образующей.

Площадь полной поверхности[править | править код]

Площадь полной поверхности цилиндра равна сумме площадей его боковой поверхности и его оснований.

Для прямого кругового цилиндра:

Объём цилиндра[править | править код]

Для наклонного цилиндра существуют две формулы:

где  — длина образующей, а  — угол между образующей и плоскостью основания. Для прямого цилиндра .

Для прямого цилиндра , и , и объём равен:

Для кругового цилиндра:

,

где d — диаметр основания.

Примечания[править | править код]

1. ↑ Математический справочник

Как проверить качество уплотнения щебеночных оснований?

Качество уплотнения щебеночного основания можно проверить с помощью нескольких методов:

1. Визуальный осмотр: при осмотре щебеночного основания внимательно проверьте наличие трещин, просадок, гребней, углублений и других дефектов, которые могут свидетельствовать о неправильном уплотнении. Правильно уплотненное основание должно быть ровным и гладким.

2. Использование виброплиты: виброплита — это специальное оборудование, которое используется для уплотнения щебеночного основания. Процесс уплотнения проводится путем проезда виброплиты по поверхности основания. При этом, уплотнение происходит за счет вибрации, которая помогает плотно уплотнить частицы щебня. Качество уплотнения можно оценить по показателям плотности и прочности основания.

3. Использование динамического конуса: динамический конус — это специальное оборудование, которое используется для оценки плотности щебеночного основания. Конус опускается на поверхность основания, затем измеряется глубина проникновения конуса. Чем глубже проникновение, тем ниже плотность щебня. Необходимо провести несколько замеров на разных участках основания.

4. Использование плотнометра: плотнометр — это специальное оборудование, которое используется для оценки плотности щебеночного основания. Он заключается в том, чтобы взвесить определенный объем щебня, который был ранее уложен на основание. Плотность рассчитывается по формуле: плотность = масса / объем.

Важно отметить, что качество уплотнения щебеночного основания зависит от многих факторов, включая тип и размер частиц щебня, тип грунта, условия окружающей среды и т.д. Поэтому, для более точной оценки качества уплотнения рекомендуется обратиться к специалистам в этой области.